
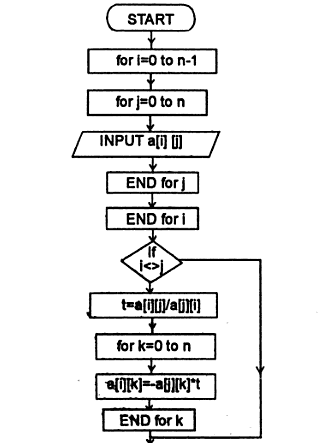
If we start with nonzero diagonal components for, then can be used to solve the system using forward substitution: The left hand side can be decomposed as follows:Įffectively, we have separated into two additive matrices: where is an upper triangular matrix with zero diagonal components, while is a lower triangular matrix with its diagonal components equal to those of the diagonal components of. First notice that a linear system of size can be written as: This is different from the Jacobi method where all the components in an iteration are calculated based on the previous iteration.

In the Gauss-Seidel method, the system is solved using forward substitution so that each component uses the most recent value obtained for the previous component. The Gauss-Seidel method offers a slight modification to the Jacobi method which can cause it to converge faster. Open Educational Resources Iterative Methods:

Cholesky Factorization for Positive Definite Symmetric Matrices.all input should be valid (n/N = ints, the rest can be floats) -> no validations were made.Numpy version 1.19.3 (previous to 1.19.4 -> had some issues initializing it).myMatrixTools.py - constains few basic matrix manipulation and analysis functions for usage.main2.py - constains larger user-input of size N, matrix a and vector b.main.py - contains basic usage demonstration of jacobi_calc() or gauss_seidel_calc(), using a 3x3 matrix, and basic arguments.rel_diff, the relative difference between last 2.If max_iter is None, the default value will set as 200. max_iter, the maxim number of possible iterations to receive the most exact solution.If tolerance is None, the default value will set as 1e-16. tolerance, the desired limitation of tolerance of solution's anomaly.If x is None, the initial guess will bw determined as a vector of 0's. if b is None - the functions returns None.

If a is None or NxM, where N != M - the functions returns None.


 0 kommentar(er)
0 kommentar(er)
